On sine and cosine

Relating the geometric intuitions of sine and cosine, to their formal expressions in terms of Taylor series.
→ [preprint] ←  #trigonometry #sine #cosine #differentiation #taylor #series

In the context of the picture below, the reader probably learned in high-school to define $\cos \theta$ and $\sin \theta$ as the $x$ and $y$ coordinates of point $P$.

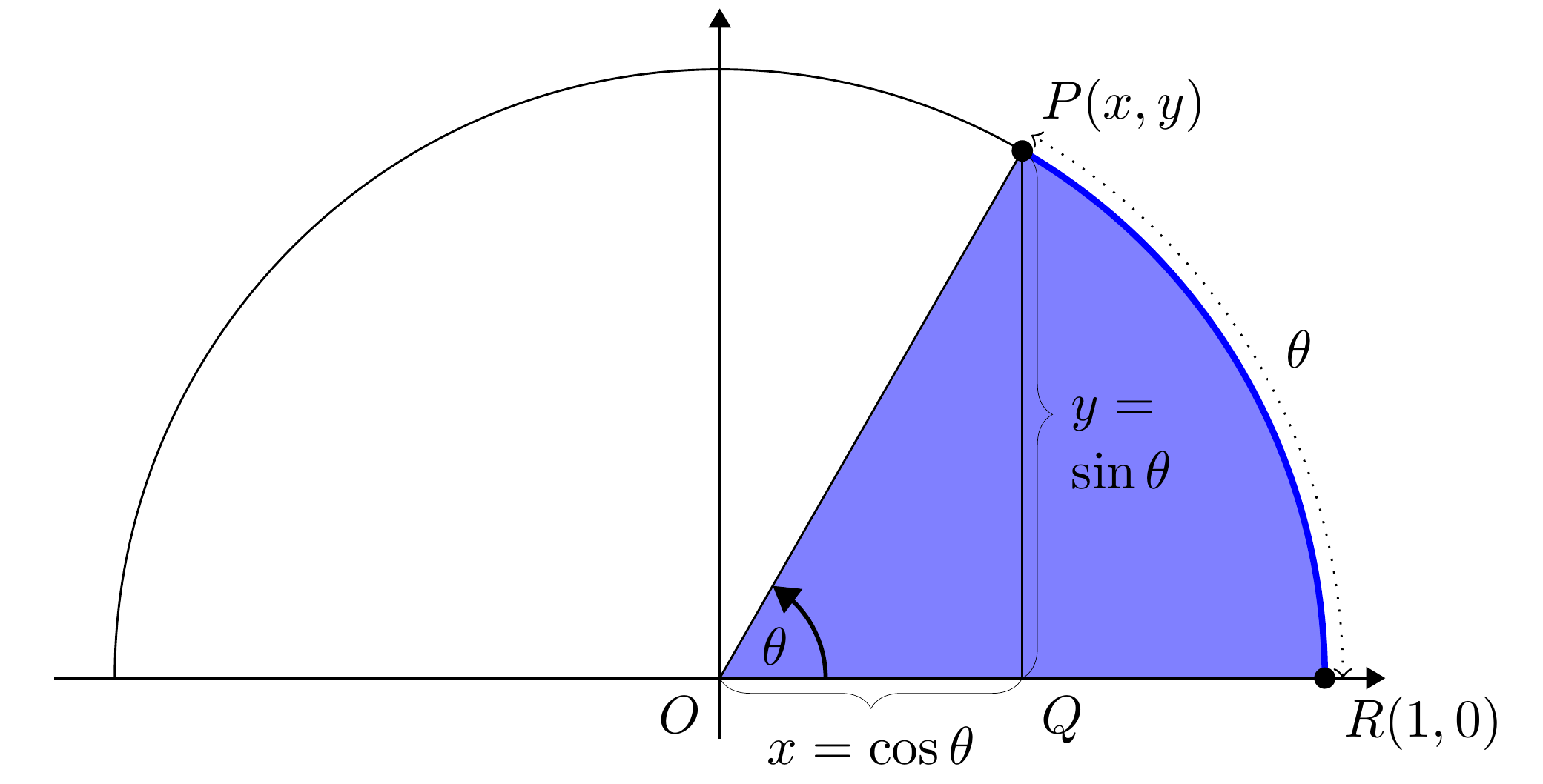
The problem is that these non-rigorous definitions, are completely detached from what one learns later (usually in undergraduate analysis), namely to define cosine and sine in terms of their Taylor series:

$$\cos x = \sum_{n = 0}^{+\infty} \left( (-1)^n \frac{x^{2n}}{(2n)!}\right) \quad \textrm{ and } \quad \sin x = \sum_{n = 0}^{+\infty} \left((-1)^n \frac{x^{2n + 1}}{(2n + 1)!} \right)$$

This paper bridges that gap, by defining $\cos \theta$ in terms of the area of the corresponding sector (in purple in the image), and from there deriving everything else: the definition of $\sin \theta$, the Taylor expansions of both, and some usual properties of these functions (e.g. the sine and cosine of sums, etc.).

August 28, 2023. Got feedback? See the contact page.

• Preprint update, February 21, 2024. Big overhaul of the paper.

  • Function $A$, the basis for defining cosine formally, is now first proved to be a bijection, which simplifies explaining why it is suited to be used to define cosine.

  • Extending sine and cosine from $[0, 2\pi]$ to all of $\mathbb{R}$ is done in a way that no longer overlaps at $2\pi$.

  • This in turn aids in explicitly proving that the derivation rules for both functions, in $]0, 2\pi[$, also apply to $\mathbb{R} \setminus {\pi}$—which is now done explicitly.

  • Added the graphs of sine and cosine, and computed their values in some frequently used points.

  • Added an appendix about triangles, and therein computed their values for some more points.

  • Added an appendix about generic properties of periodic functions.

• Preprint update, December 14, 2023. Updated the Introduction, to reflect that discussing and defining $\pi$ is only done in Section 5.

• Preprint update, December 11, 2023. The extension of sine cosine from $[0, \pi]$ to $\mathbb{R}$ is now done first, in one go. And only after that is taken care of, is continuity of both functions proved, for all of $\mathbb{R}$. In this manner it becomes simpler to follow the reasoning.

• Preprint update, December 10, 2023. Explicitly proved the continuity of sine and cosine, both going from $[0, \pi]$ to $[\pi, 2\pi]$, and then from $[0, 2\pi]$ to $\mathbb{R}$.

• Preprint update, December 9, 2023. Corrected a few typos, and clarified the derivation of sine and cosine’s Taylor expansions.

• Preprint update, October 20, 2023. Clarified the idea underlying the definition of cosine.

• Preprint update, September 2, 2023. At the end of the conclusion, $\pi$ was being defined as $\int_{-1}^{1} \sqrt{1 - t^2}dt$, which is wrong. The correct definition of $\pi$ is $2\int_{-1}^{1} \sqrt{1 - t^2}dt$. This has now been corrected.